图形结构算法

介绍

图形结构是一种比树形结构更为复杂的数据结构。在树形结构中，结点间具有分支层次关系，每一层上的结点都只能和上一层中的某个结点相关，但可能和下一层的多个结点相关。而在图形结构中，任意两个顶点之间都可能相关。因此，图形结构通常被用于描述各种复杂的数据对象，在计算机科学中有着非常广泛的应用。

树形结构用于描述结点和结点之间的层次关系，而图形结构用于描述两个顶点之间是否有连通的关系。在计算机科学中，图形结构是最灵活的数据结构之一，很多问题都可以使用图来求解。

图的定义

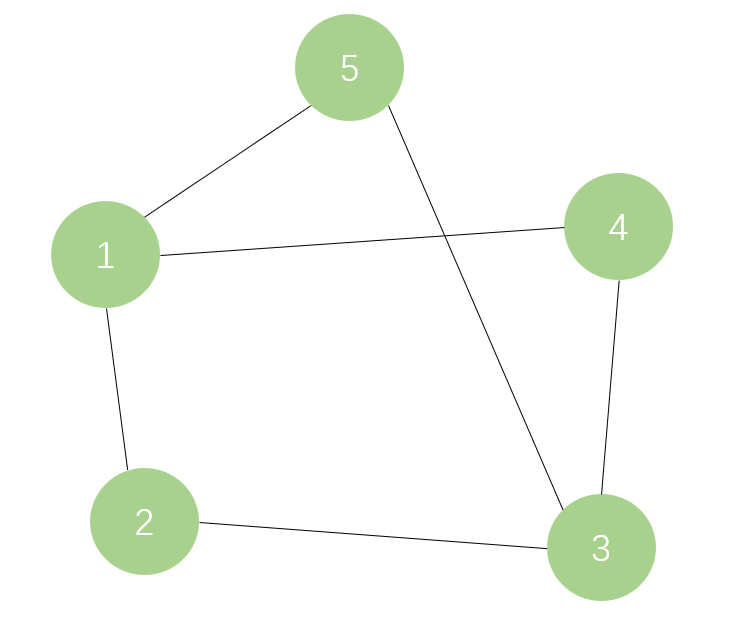
图是由顶点和连接顶点的边组成的集合。图可以表示为$G=(V,E)$，其中，G表示一个图，V表示图G中所有顶点组成的集合，E表示图G中所有边组成的集合。如图1所示的图由5个顶点和6条边组成。

图有两种，一种是无向图，一种是有向图。无向图用$(V_1,V_2)$表示，有向图用$<V_1,V_2>$表示。

1.无向图

无向图是各边都没有方向的图，同一条边的两个顶点间没有次序关系，如图1所示。例如，$(V_1,V_2)$和$(V_2,V_1)$表示的是相同的边。

2.有向图

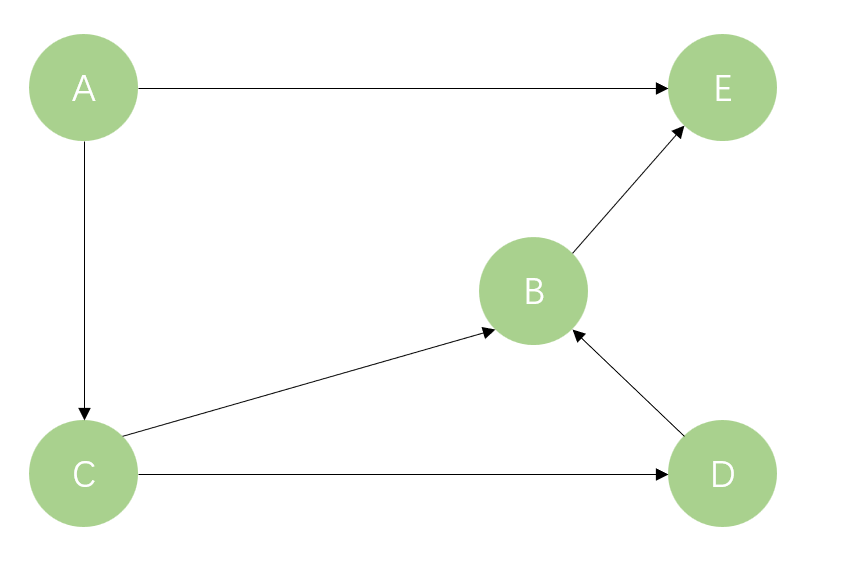
有向图是各边都有方向的图，同一条边的两个顶点之间有次序关系，如图2所示。每条边都可以用一个有序对$<V_1,V_2>$来表示。$<V_1,V_2>$表示从顶点$V_1$指向顶点$V_2$的一条边，$V_1$表示尾部，$V_2$表示头部，因此$<V_1,V_2>$和$<V_2,V_1>$表示两条不同的边。

图的相关术语

术语	含义
顶点	一个小圆点，可以是一个事物、站点或地名等
边	一个小圆点，可以是一个事物、站点或地名等
无向边	无向图中的边，即没有方向的边
有向边	有向图中的边，即有方向的边
权重	每条边上的关联数字
加权图	带权重的图
非加权图	不带权重的图
邻接	两个顶点之间的关系。如果图有边$(u,v)$，则称顶点$v$与顶点$u$邻接
关联	顶点和边之间的关系。如果图有边$(u,v)$，则称两个顶点$v$和$u$与边$(u,v)$相关联
完全图	每个顶点都与其他顶点相邻接的图
路径	依次遍历顶点序列之间的边所形成的轨迹。没有重复顶点的路径称为简单路径。路径的长度是路径上的边的数目
连通	在无向图中，如果从顶点u到顶点v有路径，则称u和v是连通的
连通图	任意两个不同顶点都是连通的无向图
生成树	以最少的边连通图中的所有顶点，且不产生回路的连通子图。生成树通常含有图中全部的n个顶点，但只有n-1条边
最小生成树	边权重之和是所有生成树中最小的树

图的遍历算法

图的遍历是指从图中的某个顶点(该顶点也可称为起始点)出发，按照某种特定方式访问图中的各顶点，使每个可访问的顶点都被访问次。图的遍历方式有两种，一种是深度优先遍历(也称为深度优先搜索，简称DFS)，还有一种是广度优先遍历(也叫作广度优先搜索，简称BFS)。

注意：起始点可以任意指定。起始点不同，得到的遍历序列也不相同。

深度优先遍历

深度遍历是经典的图论算法。其思路为：从一条路径的起始点开始追溯，直到到达路径的最后一个顶点；然后回溯，继续追溯下一条路径，直到到达最后的顶点；如此往复，直到没有路径为止。其遍历过程如下：

（1）以图中任一顶点$v$为出发点，首先访问顶点$v$，将其标记为已被访问。

（2）从顶点$v$的任一邻接点出发，继续进行深度优先搜索，直至图中所有和顶点$v$连通的顶点都已被访问。

（3）若此时图中仍有未被访问的顶点，则选择一个未被访问的顶点作为新的出发点，重复上述过程，直至图中所有顶点都已被访问为止。

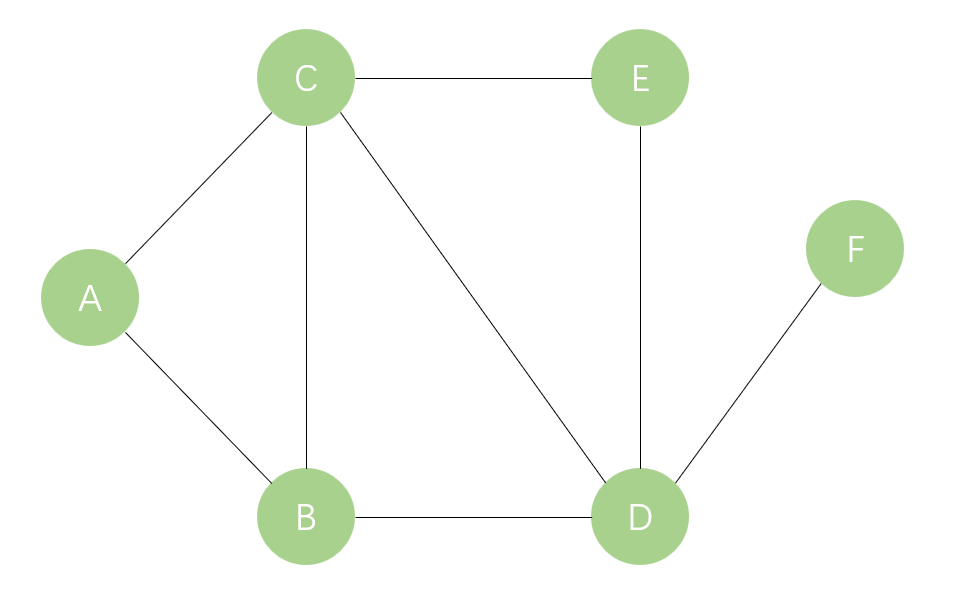
深度优先遍历应用了堆栈数据结构。下面以如图3所示的无向图为例，介绍具体的遍历过程。

（1）假设以顶点A为起点，将顶点A压入栈，如堆栈图1所示。

（2）弹出顶点A，将顶点A的邻接点B
和C压入堆栈，如堆栈图2所示。

（3）根据堆栈“后进先出”的原则，弹出顶点C,将与顶点C相邻且未被访问过的顶点B、顶点D和顶点E压入堆栈，如堆栈图3所示。

（4）弹出顶点E，将与顶点E相邻且未被访问过的顶点D压入堆栈，如堆栈图4所示。

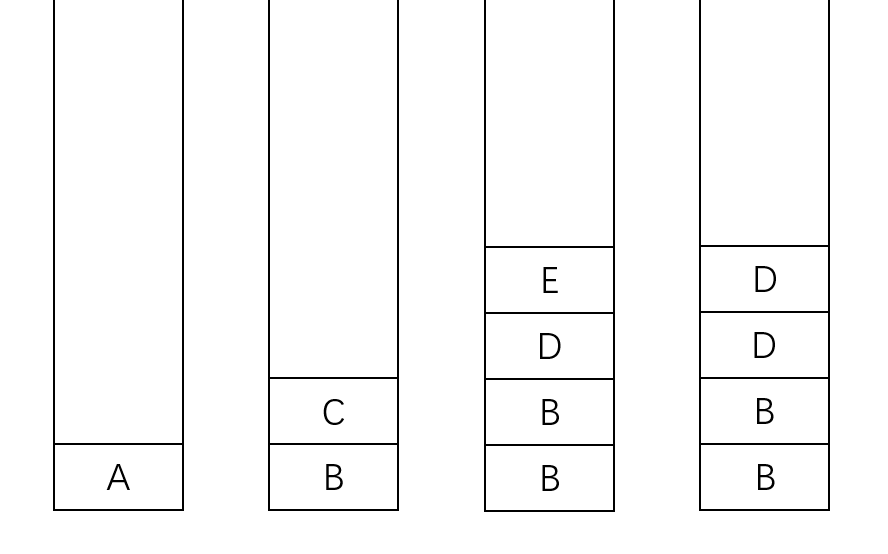
（5）弹出顶点D,将与顶点D相邻且未被访问过的顶点B和顶点F压入堆栈，如堆栈图5所示。

（6）弹出顶点F,由于顶点F的邻接点D已被访问过，所以无须压入堆栈，如堆栈图6所示。

（7）弹出顶点B,由于顶点B的邻接点都已被访问过，所以无须压入堆栈，如堆栈图7所示。

（8）将堆栈中的顶点依次弹出，并判断是否已经访问过，直到堆栈中无顶点可以访问为止，如堆栈图8所示。

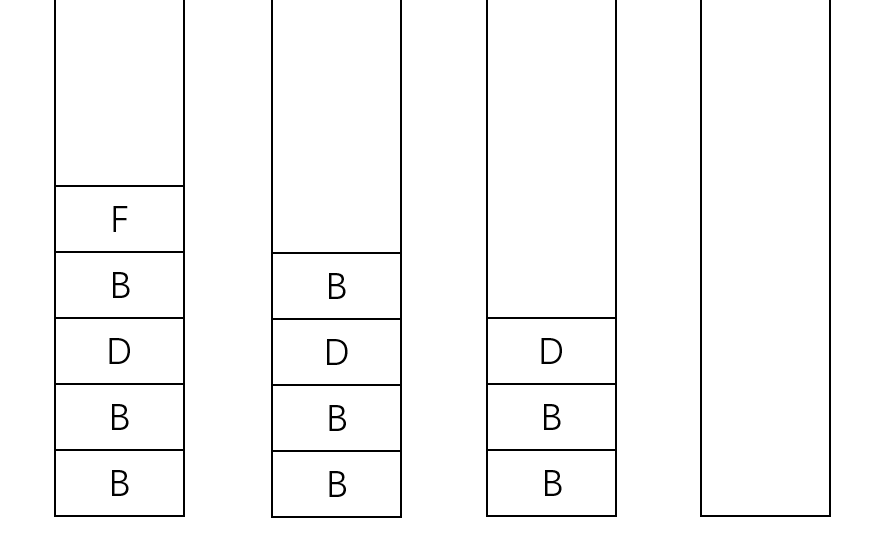
由此可知，对图3的无向图进行深度优先遍历的顺序为：顶点A、顶点C、顶点E、顶点D、顶点F、顶点B。

应用深度优先算法的函数如下：

def dfs(graph, start):
    stack = []
    stack.append(start)
    visited = set()  # 定义集合
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            visited.append(vertex)  # 将该顶点放入已访问集合
            print(vertex, end=" ")
        for w in graph[vertex]:  # 遍历相邻顶点
            if w not in visited:
                stack.append((w))  # 把顶点压入栈

广度优先遍历

广度优先遍历应用的是队列这种数据结构。其遍历结果如下：

（1）以图中的任一顶点$v$为出发点，首先访问顶点$v$。

（2）访问顶点v的所有未被访问过的邻接点$v_1,v_2,…,v_n$。

（3）按照$v_1,v_2,…,v_n$的次序，访问每个顶点的所有未被访问过的邻接点。

（4）以此类推，直到图中所有和顶点$v$连通的顶点都被访问过为止。

下面以图4所示的无向图为例，介绍广度优先遍历的具体过程。

（1）假设以顶点A为起点，将顶点A放入队列，如队列图1所示。

（2）取出顶点A，将顶点A的邻接点B和C放入队列，如队列图2所示。

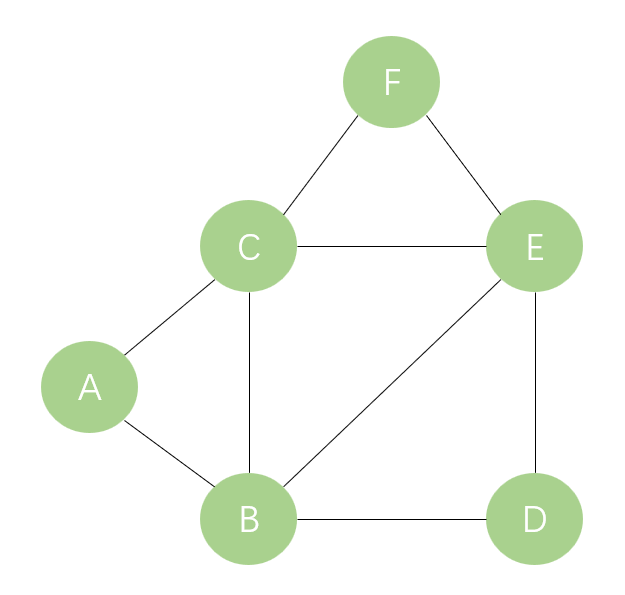
（3）根据队列“先进先出”的原则，取出顶点B，将与顶点B相邻且未被访问过的顶点D和顶点E放入队列，如队列图3所示。

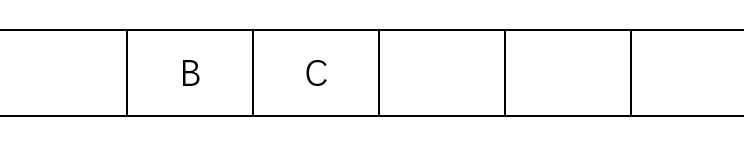
（4）取出顶点C，将与顶点C相邻且未被访问过的顶点F放入队列，如队列图4所示。

（5）取出顶点D，由于顶点D的邻接点B和E都已被访问过，所以无须放入队列中，如队列图5所示。

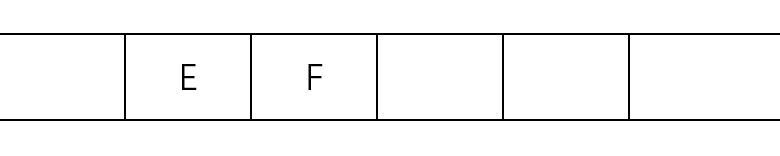
（6）取出顶点E，由于顶点E的4个邻接点都已被访问过，所以无须放入队列中，如队列图6所示。

（7）取出顶点F，由于顶点F的邻接点C和E都已被访问过，所以无须放入队列中，如队列图7所示。

这时，队列中的值都已被取出，表示图中的顶点都已被访问过。由此可知，对图4进行广度优先遍历的顺序为：顶点A、顶点B、顶点C、顶点D、顶点E、顶点F。

应用广度优先算法的函数如下：

def bfs(graph, start):
    queue = []
    queue.append(start)
    visited = set()  # 定义集合
    visited.add(start)  # 将起始顶点放入已访问集合
    while queue:
        vertex = queue.pop(0)  # 取出队列第一个元素
        print(vertex, end=" ")
        for w in graph[vertex]:  # 遍历相邻顶点
            if w not in visited:
                visited.add(w)
                queue.append((w))  # 把顶点放入队列