并查集

什么是并查集

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

并查集支持两种操作：

• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

适用条件

并查集用在一些有$n$个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这个过程看似并不复杂，但数据量极大，若用其他的数据结构来描述的话，往往在空间上过大，计算机无法承受，也无法在短时间内计算出结果，所以只能用并查集来处理。

初始化

每一个祖先都是自己。

int fa[MAXN];
void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
    }
}

查询操作

我们用递归的写法实现对代表元素的查询：一层一层的访问父节点，直至根节点（根节点的标志就是父节点是本身）。要判断两个元素是否属于同一个集合，只需要看它们的根节点是否相同即可。

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
        return find(fa[x]);
}

合并操作

先找到两个集合的根节点，然后将前者的父节点设为后者即可。当然也可以将后者的父节点设为前者。

void merge(int i, int j)
{
    i=find(i);
    j=find(j);
    if (i!=j)
    {
        fa[i]=j;
    }
}

下面我们举个例子来具体说明这些操作:

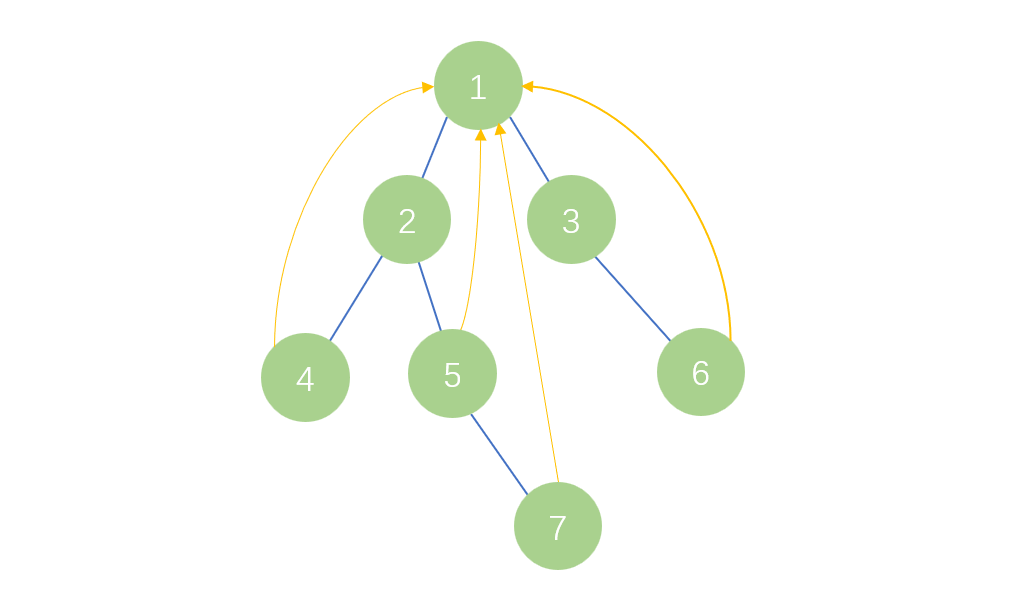
如图一，开始时我们有一些散乱的无连接的点集，我们将其初始化为7个集合，即每个点的根节点均为自己本身。

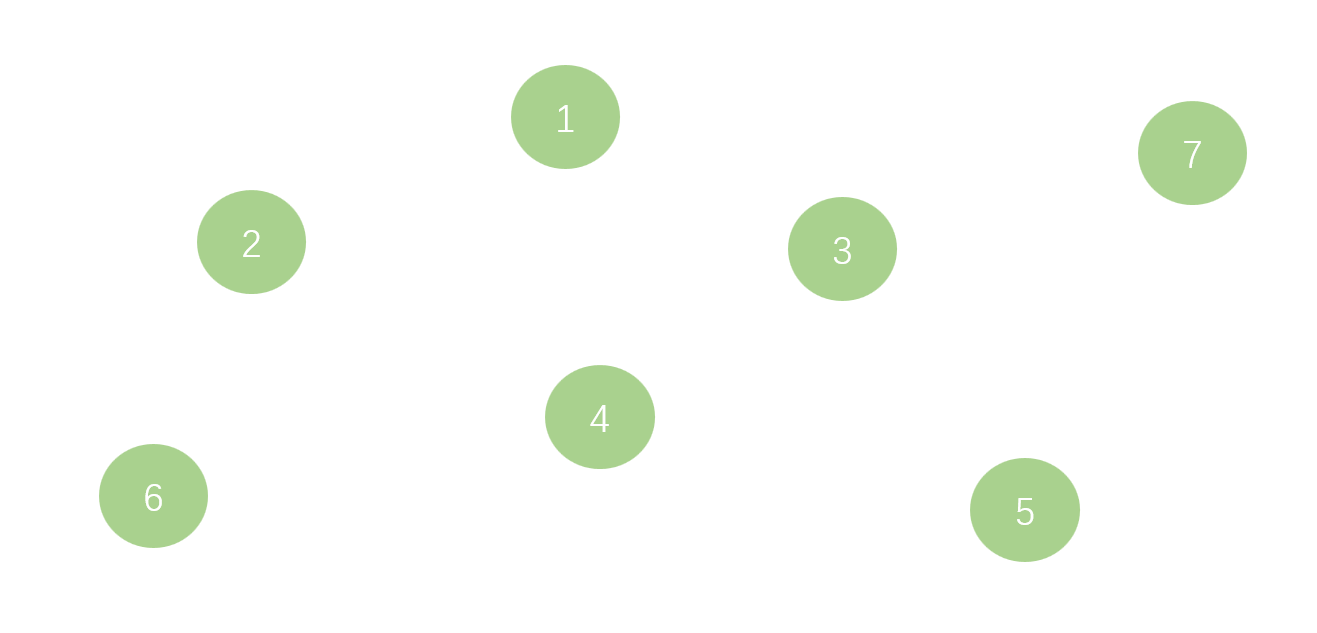
接着我查询1，2号是否在同一个集合下，发现不是。接着我们想要将1，2号合并，于是将2号的父节点设为1号；查询4，6号是否在同一个集合下，发现不是，将4，6号合并，将6号的父节点设为4号，如图二。

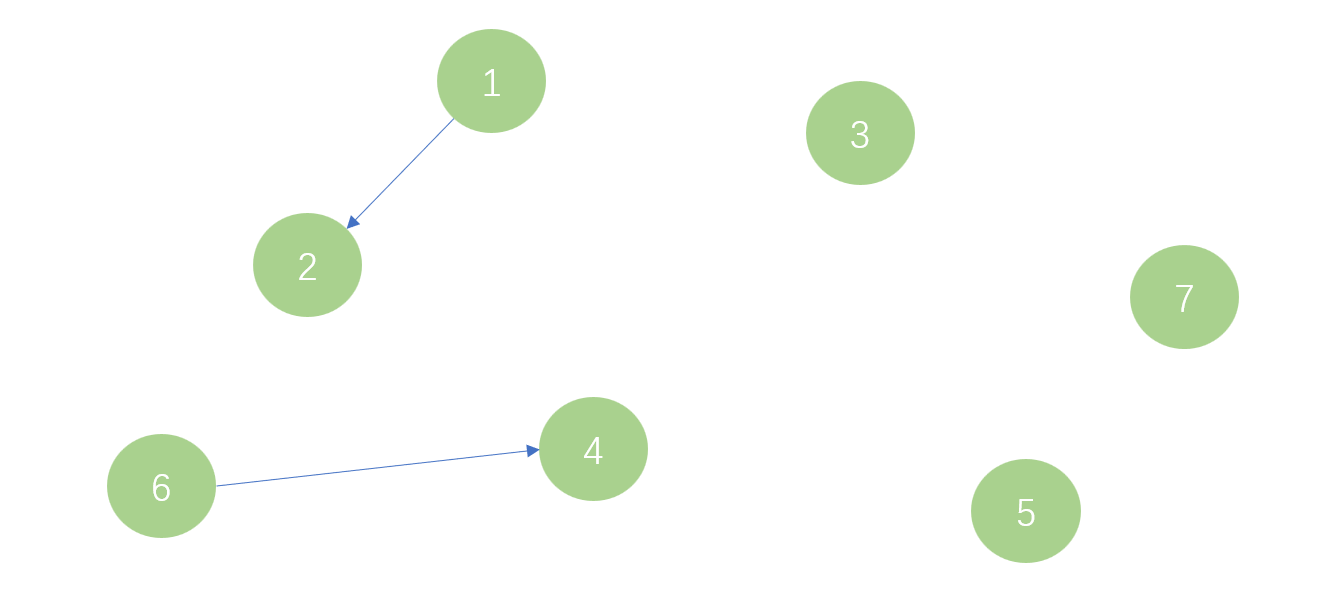
接着我分别查询3，5号以及3，7号是否在同一个集合下，发现不是，于是将3，5号、3，7号合并，将5号，7号的父节点设为3号，如图三。

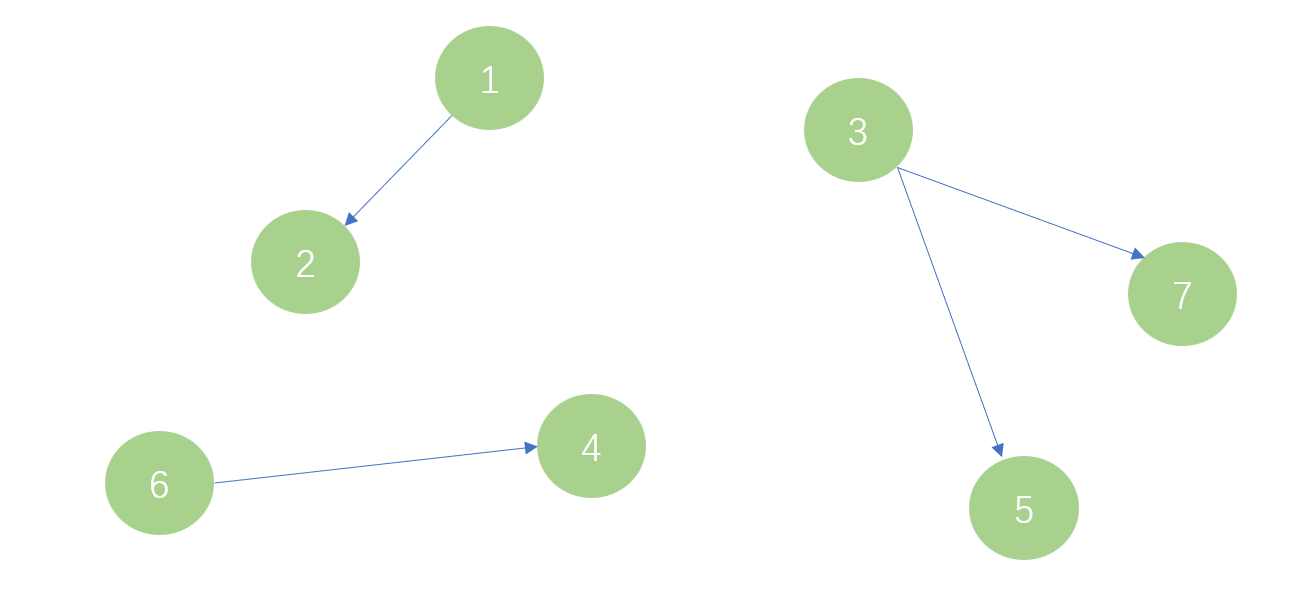
同理，将3号的父节点设为1号，如图四。

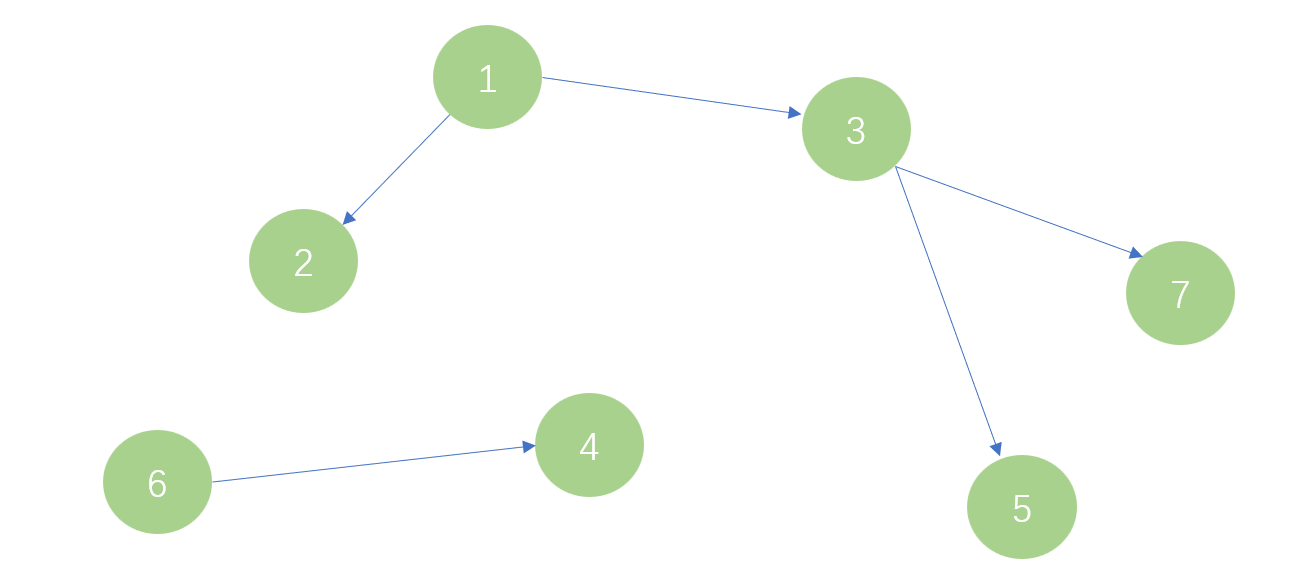
路径压缩

随着元素的不断加入，集合会变得越来越大，链子也会越来越长，这会对我们的查询操作产生影响，查询的效率降低。我们可以在每次查询的时候将每个经过的结点的父节点设为根节点，下次在查询时就可以节省很多时间。

int find(int x)
{
    if (x==fa[x])
    {
        return x;
    }
    else
    {
        fa[x]=find(fa[x]);
        return fa[x];
    }
}

按秩合并

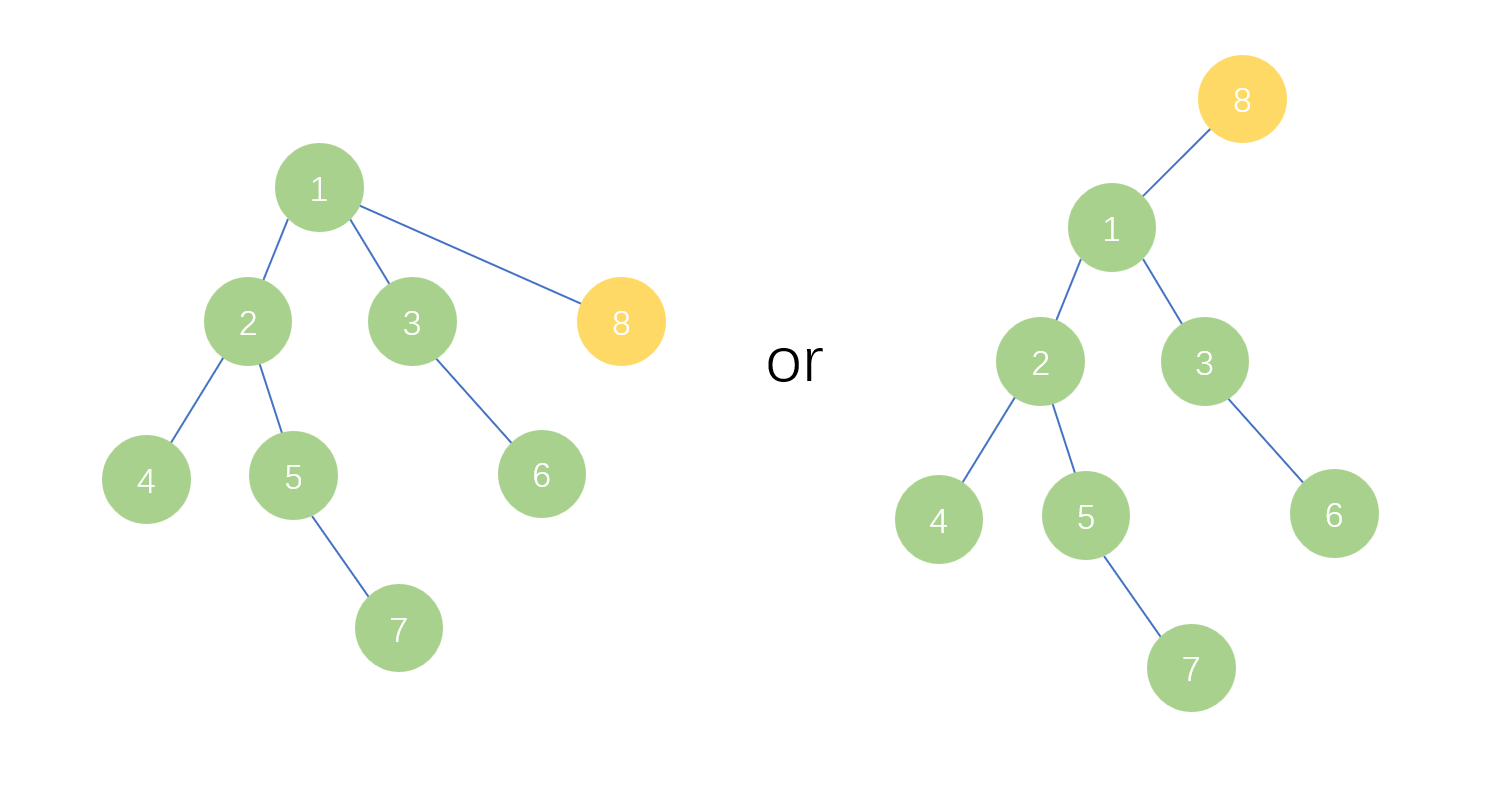
针对合并函数merge()，往往有两种合并方式，即把$a$节点的父节点设为$b$和把$b$节点的父节点设为$a$，很显然，两种合并方式的结果并不同，合并后整体的查询效率也不同。如图六，绿色和黄色对应两棵树，图中的第一种合并方式下只有8号的查询需要多一步，而第二种方式下除了8号的所有元素查询都要增加一步。

因此，我们需要定义一个判断条件：秩。秩可以是很多因素，比如树高，节点个数，等等。不管选择什么作为秩，合并时都最好要遵循启发式合并的原则，即将小的集合合并到大的集合中。下面以秩为树高来举例。

初始化

int rank[2000]={0};

void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
        rank[i]=1;
    }
}

按秩合并

void merge(int i, int j)
{
    i=find(i);
    j=find(j);
    if (i!=j)
    {
        if (ra[i]<=ra[j])
        {
            fa[i]=j;
        }
        else
        {
            fa[j]=i;
        }
        if (ra[i]==ra[j])
        {
            ra[j]++;
        }
    }
}