01trie

01 trie树

类似于字典树的做法，将每一个数化为二进制数，看作01串，插入到字典树中。如图1：

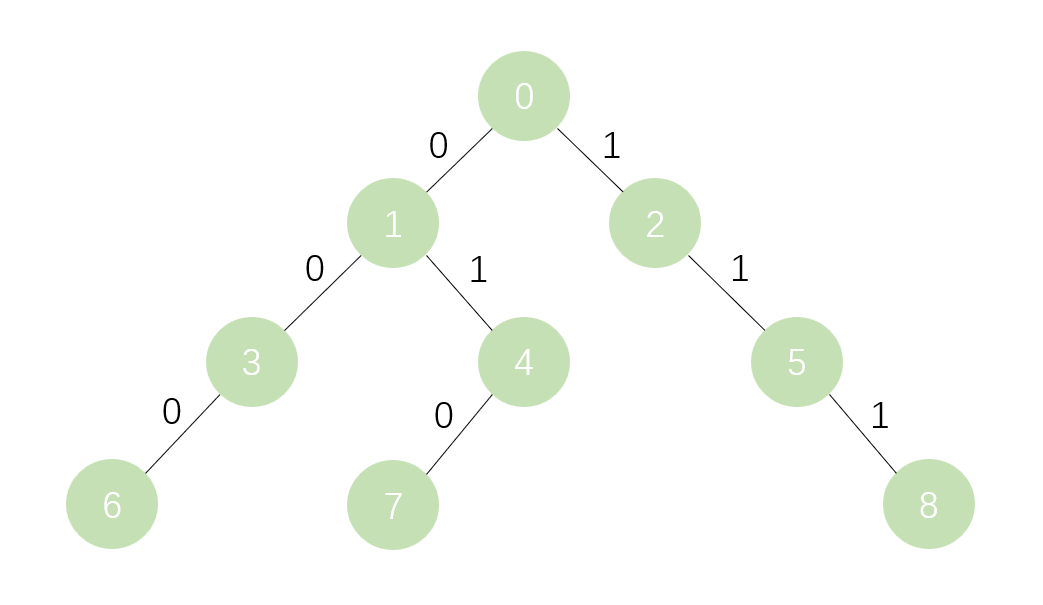
典型例题

给一个长为$n$的数列，要求一个 $a_i$，$a_j$ ，使得 $a_i$^$a_j$ 最大。

异或的一些性质

• 0^1=1
• 1^1=0
• 0^0=0
• p^p=0
• p^0=1
• 自反性：a^b=c，b^c=a

问题解答

首先建好01trie树，以图1为例，然后对于每一个数，在树上跑一遍贪心，即贪心选择与这个数当前位不同的那个节点。

也就是说，尽可能地保证越高的位的异或和为1，（因为高位的一个1比后面的位全为1都要大）

比如对于7，在下面这个插入了0，2，7的树上跑。
开始在0号节点，然后看最高位，7的最高位是1，所以为了保证当前位异或和为1，应走0的方向，也就是走到1节点。
然后看次高位，7的次高位为1，同理，走0的方向到3号节点，依次类推，得出与7异或的最大值为7。

两道拓展例题

1.第k大异或和

题意：还是给出长为$n$的序列，这次不求最大值了，求第$k$大的$a_i$^$a_j$。

做法：考虑二分答案，对于每个二分到的值$x$，遍历数组跑一遍01trie树，看有多少组异或和是大于$x$的，然后根据大于$x$的异或和的组数向上向下二分。

如何计算大于$x$的组数？

遍历数组，对于每一个数$a_i$,跑一遍01trie，记录比$x$大的异或和的组数$ans$。对于$x$的每一位，若为1，则走树上与$a_i$当前位相反的位置，若为0，则走树上与$a_i$当前位相同的位置，并将与$a_i$当前位相反的那个位置的子树大小加到$ans$中。

由于每一组大于$x$的二元组都会被计算两次，所以最终的$ans$还要除以二。

复杂度$O(nlogn)$。

2.树上的最大异或路径和

题意：给定一棵$n$个点的带权树，寻找树中找两个结点，求最长的异或路径。异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

做法：观察得到，从$i$~$j$的路径的异或值为$i$到根的异或和^$j$到根的异或和。

因此将例题中的$a_i$转化成节点$i$到根的异或和的值，就可以照着例题的方法做了。

复杂度$O(nlogn)$。