贪心算法
介绍
贪心算法（英语：greedy algorithm），又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是问题能够分解成子问题来解决，子问题的最优解能递推到最终问题的最优解。
贪心法是解决问题的一种策略。如果策略正确，那么贪心法往往是易于描述、易于实现的。
经典问题
1.背包相关问题
最优装载问题/部分背包问题
此类问题较简单，按题意逐步选择最优解即可。
乘船问题
有n个人，第$i$个人重量为$wi$。每艘船的最大载重量均为$C$，且最多只能乘两个人。用最少的船装载所有人。
【分析】考虑最轻的人$i$，他应该和谁一起坐呢？如果每个人都无法和他一起坐船， 则唯一的方案就是每人坐一艘船。否则，他应该选择能和他一起坐船的人中最重的一个$j$。这个贪心策略是对的，可以用反证法证明。
上实战：https://www.luogu.com.cn/problem/P1094
2.区间相关问题
选择不相交区间
数轴上有n个开区间$(a,b)$。选择尽量多个区间，使得这些区间两两没有公共点。
【分析】
1.小区间被大区间包含，这种情况下一定不会选大区间。
2.排除情况一，对右端点进行从小到大排序，然后依次遍历，如果能选进来就选。
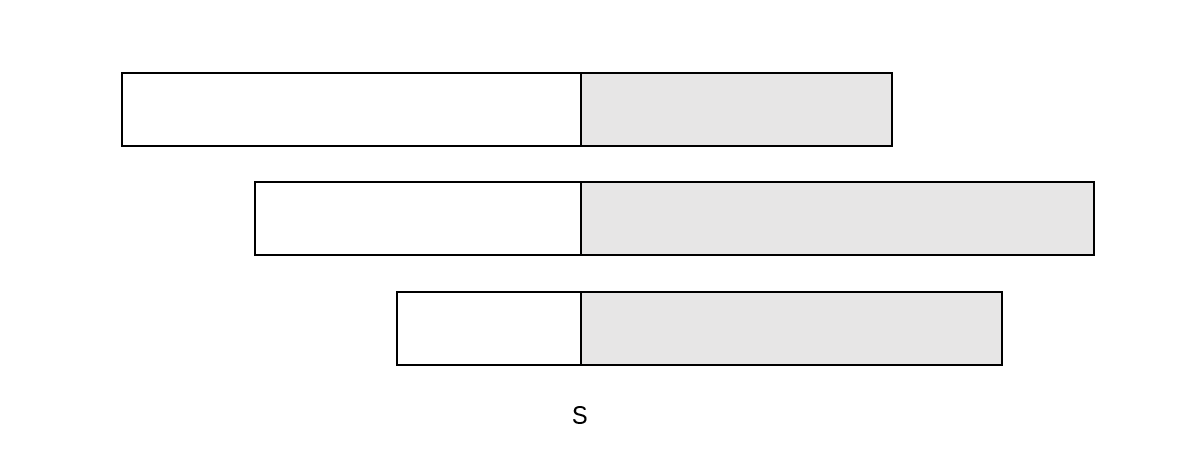
区间选点问题
数轴上有n个闭区间$[ai,bi]$。取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）。
【分析】
1.小区间被满足时大区一定也被满足，所以在区间包含的情况下，大区间不需要考虑。
2.把区间按$b$从小到大的顺序（$b$相同时$a$从大到小排序），取第一个区间的最后一个点。因为最后一个点和中间的点相比被满足的区间增加了，而且原来满足的区间现在一定也满足。
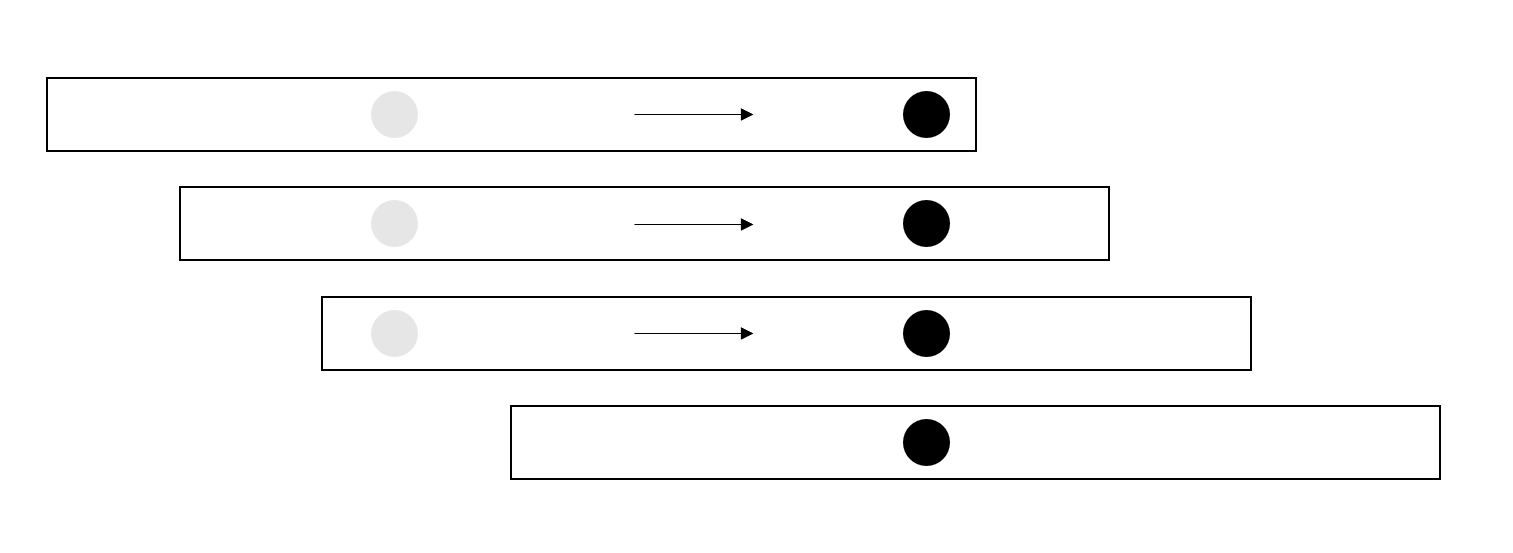
区间覆盖问题
数轴上有n个闭区间$[ai,bi]$，选择尽量少的区间覆盖一条指定的线段$[s,t]$。
【分析】
1.由于再区间$[s,t]$外的部分毫无意义，所以不必考虑这些部分。再区间[$s,t]$的范围内，显然被大区间包含的小区间不应该考虑。
2.把各区间按$a$从小到大的顺序排序。如果排在第一个的区间的起点不是$s$，无解。否则选择起点在$s$的最长区间（即从$s$开始覆盖区间[$s,t]$的求最大范围的区间）。选择区间$[ai,bi]$后，新的起点应该为$bi$，重复先前操作。
3.Huffman编码
假设某文件只有6种字符：a，b，c，d，e，f，可以用3个二进制位来表示，如表。
| 字符 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 频率 | 45 | 13 | 12 | 16 | 9 | 5 |
| 编码 | 000 | 001 | 010 | 011 | 100 | 101 |
这样，一共需要（45+13+12+16+9+5）*3=300比特。
接下来我们用 变长码 。
| 字符 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 频率 | 45 | 13 | 12 | 16 | 9 | 5 |
| 编码 | 0 | 101 | 100 | 111 | 1101 | 1100 |
总长度为145+313+312+316+49+45=224比特，比 定码 短。
下表是错误的变长码。
| 字符 | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 频率 | 45 | 13 | 12 | 16 | 9 | 5 |
| 编码 | 0 | 1 | 00 | 01 | 10 | 11 |
虽然总长度只有142比特，但是很可惜，这种编码方式有问题。假设我们接收到001，那么我们无法判断他到底是aab、cb还是ad。也就是说，这种编码方式会造成歧义，因为其中一个字符的编码是另一个字符编码的前缀。这里把满足这种性质的编码成为前缀码（Prefiix Code）。下面我们来正式叙述编码问题。
最优编码问题
给出n个字符的频率$ci$，给每一个字符赋予一个01编码串，使得每一个字符的编码不是另一个字符编码的前缀，而且编码后占用的空间（每个字符的频率*该字符编码长度）尽可能小。
【分析】在解决这个问题之前，首先来看一个结论：任何一个前缀编码都可以表示成每个非叶节点恰好有两个子节点的二叉树。如图，每个非叶节点与左子节点的边上写上1，与右节点的边上写上0。
每个叶子对应一个字符，编码为从根节点到该叶子的路径上的01序列。如图，N的编码为001，E的编码为11。为了证明在一般情况下，都可以用这样的二叉树来表示最优前缀码，需要证明两个结论。
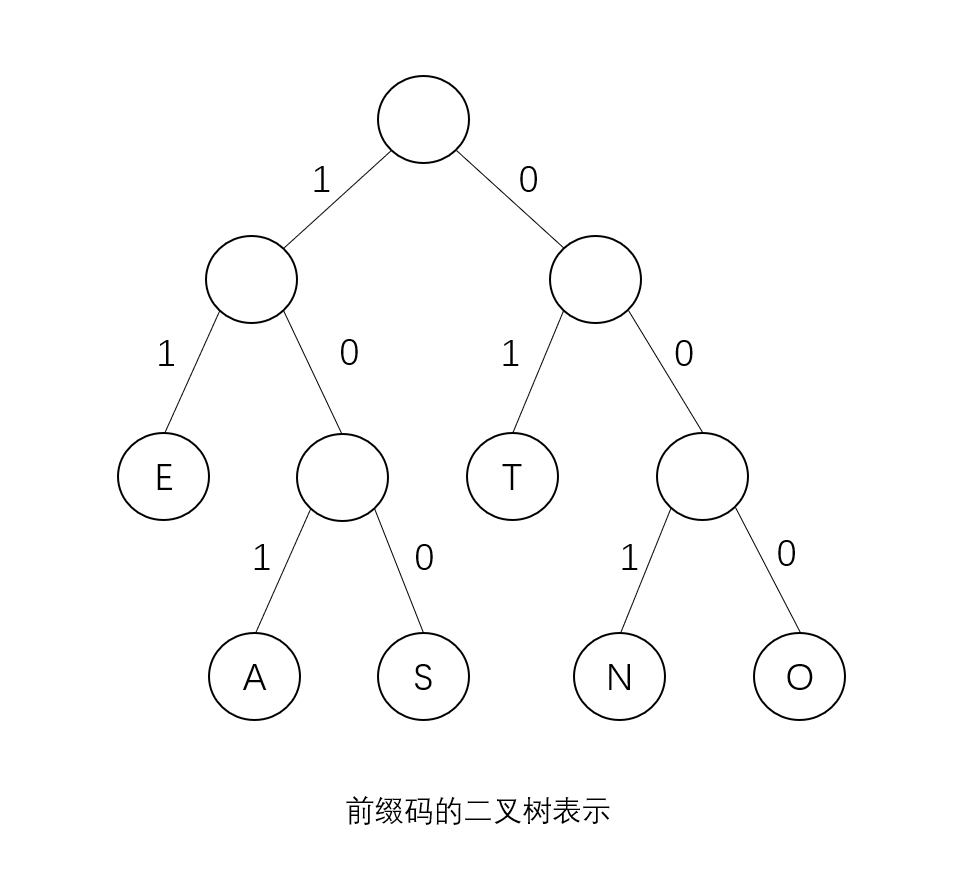
- 结论1：n个叶子的二叉树一定对应一个前缀码。如果编码$a$为编码$b$的前缀，则$a$所对应的节点一定为$b$所对应的节点的祖先。而两个叶子不会有祖先后代的关系。
- 结论2：最优前缀码定可以写成二义树。逐个字符构造即可。每拿到一个编码，都可构造出从根到叶子的一条路径，沿着已有结点走，创建不存在的结点。这样得到的二叉树不可能有单子结点，因为如果存在，只要用这个子结点代替父结点，得到的仍然是前缀码，且总长度更短。
接下来的问题就变成：如何构造出一颗最优的编码树。
Huffman算法
把每个字符看作一个 单节点子树放在一个树集合中，每棵子树的权值等于相应字符的频率。每次取权值最小的两棵子树合并成一棵新树， 并重新放到集合中。新树的权值等于两棵子树权值之和。
下面分两步证明算法的正确性。
结论1：设$x$和$y$是频率最小的两个字符，则存在前缀码使得x和y具有相同码长，且仅有最后一位编码不同。换句话说，第一步贪心法选择保留最优解。
证明：假设深度最大的节点为$a$,则$a$一定有一个兄弟$b$。不妨设$f(x)≤f(y)$，$f(a)≤f(b)$，则$f(x)≤f(a)$，$f(y)≤f(b)$。如果$x$不是$a$，则交换$x$和$a$；如果$y$不是$b$,则交换$y$和$b$。这样得到的新编码树不会比原来的差。
结论2：设$T$是加权字符集$C$的最优编码树，$x$和$y$是树$T$中两个叶子，且互为兄弟节点，$z$是它们的父节点。若把$z$看成具有频率$f(z)=f(x)+f(y)$的字符，则树$T’=T-｛x,y｝$是字符集$C’=C-｛x,y｝∪｛z｝$的一棵最有编码树。换句话说，原问题的最优解包含子问题的最优解。
证明：设$T’$的编码长度为$L$，其中字符$｛x,y｝$拆成2个后，长度变为$L-(f(x)+f(y))h+(f(x)+f(y))(h+1)=l+f(x)+f(y)$。因此$T’$必须是$C’$的最优编码树，$T$才是$C$的最优编码树。
结论1通常称为贪心选择的性质，结论2常称为最优子结构性质。根据这两个结论，Huffman算法正确。在程序的实现上，可以先按频率把所有字符排序成表$P$，然后创建一个新节点队列$Q$，在每次合并两个节点后把新节点放在队列$Q$中。由于后合并的频率和一定比先合并的频率和大，因此$Q$内的元素是有序的。类似有序表的合并过程，每次只需要检查$P$和$Q$的首元素即可找到最小的元素，时间复杂度为$O(n)$。算上排序，总时间复杂度为$O(n logn)$。
核心思想
贪心算法的核心在于将全局最优解分解为局部最优解，但是很多时候容易过早做出决定，从而无法达到最优解。这些问题往往比较考察思维能力，判断局部最优解能否达到全局最优解尤为重要。
常见方法
1.排序解法
用排序法常见的情况是输入一个包含几个（一般一到两个）权值的数组，通过排序然后遍历模拟计算的方法求出最优值。
2.后悔解法
思路是无论当前的选项是否最优都接受，然后进行比较，如果选择之后不是最优了，则反悔，舍弃掉这个选项；否则，正式接受。如此往复。